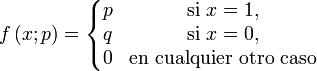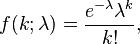Distribuciones Discretas





Definición:
. Las Distribuciones Discretas de probabilidad son funciones que presentan siempre una característica determinada.

Al tener conocimiento pleno de estas se podrá encontrar la función de distribución acumulada de la distribución discreta, el valor esperado o media de la distribución discreta, así como la variancia de la distribución discreta.
Una variable discreta es sencillamente una variable para la que se dan de modo inherente separaciones entre valores observables sucesivos. En otraspalabras, se define una variable discreta como la variable tal que entre 2 valores cualesquiera observables, hay por lo menos un valor no observable.



-Resumen-

Primeramente se estudia la distribución binomial, así como la distribución de Poisson y su utilización como una aproximación de la distribución binomial.
Tambien es mencionada dentro del tema la distribución geometrica y por ultimo la no menos importante distribución hipergeométrica.



Distribución de Bernoulli



La distribución de Bernoulli (o distribución dicotómica), nombrada así por el matemático ycientífico suizo Jakob Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito (p) y valor 0 para la probabilidad de fracaso (q = 1 − p).
Si X es una variable aleatoria que mide "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria X se distribuye como una Bernoulli de parámetro p.
X˜Be(p)
La fórmula será:
f(x) = px(1 − p)1 − x con x = {0,1}

Su función de probabilidad viene definida por:

f\left(x;p\right) = \left\{\begin{matrix} p & \mbox {si }x=1, \\ q & \mbox {si }x=0, \\ 0 & \mbox {en cualquier otro caso}\end{matrix}\right.

Un experimento al cual se aplica la distribución de Bernoulli se conoce como Ensayo de Bernoulli o simplemente ensayo, y la serie de esos experimentos como ensayos repetidos.



Distribución de Poisson




La distribución de Poisson es una distribución de probabilidaddiscreta. asi tiempo fijo si estos eventos ocurren con una frecuencia media conocida y son independientes del tiempo discurrido desde el último evento.

a función de masa de la distribución de Poisson es
f(k;\lambda)=\frac{e^{-\lambda} \lambda^k}{k!},\,\!
donde λ es un parámetro positivo que representa la frecuencia esperada del fenómeno modelado por la distribución.
Tanto el valor esperado como la varianza de una variable aleatoria con distribución de Poisson son iguales a λ. Los momentos de orden superior son polinomios de Touchard en λ cuyos coeficientes tienen una interpretacióncombinatorio. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces según lafórmula de Dobinski, el n-ésimo momento iguala al número de particiones de tamaño n.
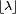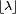La moda de una variable aleatoria de distribución de Poisson con un λ no entero es igual a \scriptstyle\lfloor \lambda \rfloor, el mayor de los enteros menores que λ (los símbolos \scriptstyle\lfloor \rfloor representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.
La función generadora de momentos de la distribución de Poisson con valor esperado λ es
\mathrm{E}\left(e^{tX}\right)=\sum_{k=0}^\infty e^{tk} f(k;\lambda)=\sum_{k=0}^\infty e^{tk} {\lambda^k e^{-\lambda} \over k!} =e^{\lambda(e^t-1)}.
Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.



Suscribirse a: Entradas (Atom)