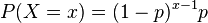Distribuciones Discretas

Una distribución de probabilidad es considerada binomial cuando se realizan n ensayos repetidos de Bernoulli.
Es importante señalar que los cofactores de las probabilidades son los términos sucesivos del desarrollo del coeficiente binomial. En un problema binomial la variable aleatoria X es el número de éxitos independientes en n ensayos, lo que permite identificarla fácilmente.
Los problemas binomiales deben cumplir con las condiciones siguientes:
-       Existe Independencia en n ensayos.
-       En cada ensayo existen solo 2 resultados, p de éxito y q de fracaso.
-       Las pruebas son con remplazo.
-       Los n ensayos se repiten.
-       La probabilidad de un éxito permanece constante en cada prueba.

Media
La Media de la distribución binomial B(x n p) esta dada por
μ=np


Varianza
La varianza se representa por V(x) ó σ2, está definida por
V(x)=npq







Distribución Geométrica

 La distribución geométrica es cualquiera de las dos distribuciones de probabilidad discretas siguientes:
  • la distribución de probabilidad del número X del ensayo de Bernoulli necesaria para obtener un éxito, contenido en el conjunto { 1, 2, 3,...} o
  • la distribución de probabilidad del número Y = X − 1 de fallos antes del primer éxito, contenido en el conjunto { 0, 1, 2, 3,... }.
Cual de éstas es la que uno llama "la" distribución geométrica, es una cuestión de convención y conveniencia.


Propiedades

Si la probabilidad de éxito en cada ensayo es p, entonces la probabilidad de que x ensayos sean necesarios para obtener un éxito es
P(X = x) = (1 - p)^{x-1}p\,
para x = 1, 2, 3,.... Equivalentemente, la probabilidad de que haya x fallos antes del primer éxito es
P(Y=x) = (1 - p)^{x} p\,
para x = 0,1, 2, 3,....
En ambos casos, la secuencia de probabilidades es una progresión geométrica.
El valor esperado de una variable aleatoria X distribuida geométricamente es
\ E(X) = \frac{1}{p}.
y dado que Y = X-1,
\ E(Y) = \frac{1-p}{p}.
En ambos casos, la varianza es
\mbox{var}(Y) = \mbox{var}(X) = \frac{1-p}{p^2}.
Las funciones generatrices de probabilidad de X y la de Y son, respectivamente,
G_X(s) = \frac{sp}{1-s(1-p)} \quad \textrm{y} \quad G_Y(s) = \frac{p}{1-s(1-p)}, \quad |s| < (1-p)^{-1}.
Como su análoga continua, la distribución exponencial, la distribución geométrica carece de memoria. Esto significa que si intentamos repetir el experimento hasta el primer éxito, entonces, dado que el primer éxito todavía no ha ocurrido, la distribución de probabilidad condicional del número de ensayos adicionales no depende de cuantos fallos se hayan observado. El dado o la moneda que uno lanza no tiene "memoria" de estos fallos. La distribución geométrica es de hecho la única distribución discreta sin memoria.
De todas estas distribuciones de probabilidad contenidas en {1, 2, 3,... } con un valor esperado dado μ, la distribución geométrica X con parámetro p = 1/μ es la de mayor entropía.
La distribución geométrica del número y de fallos antes del primer éxito es infinitamente divisible, esto es, para cualquier entero positivo n, existen variables aleatorias independientes Y1,..., Yn distribuidas idénticamente la suma de las cuales tiene la misma distribución que tiene Y. Estas no serán geométricamente distribuidas a menos que n = 1.
Suscribirse a: Entradas (Atom)